Healthcare Variation and Physician Agency

Author

Ian McCarthy | Emory University

Outline

  1. Motivation
  2. Physician Agency
  3. Policy Issures

Motivation

Variation in care

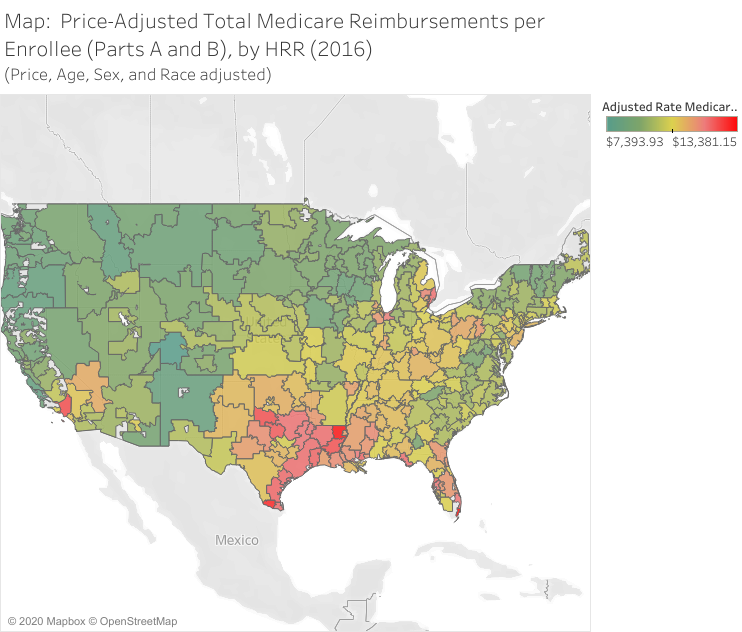
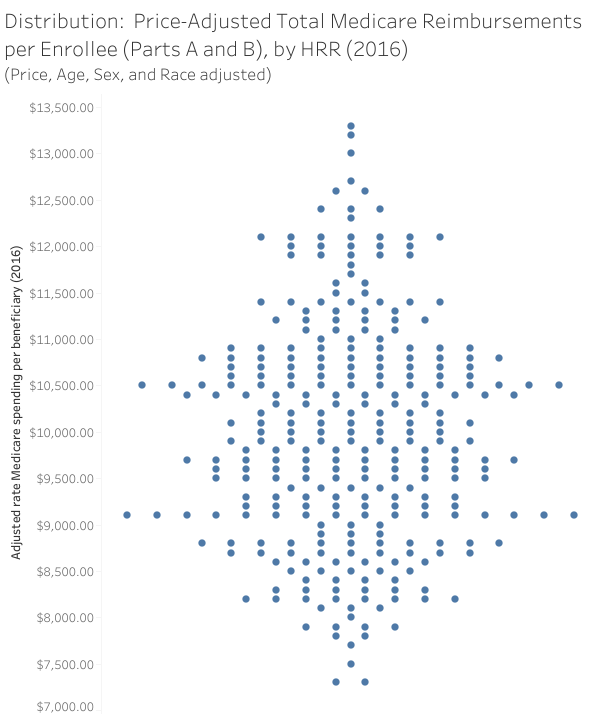
Wasteful?

  • Estimates are that more than 30% of health care expenditures are “wasteful”: (The Atlantic, 2013)
  • Some clear areas of waste:
    • Payment differentials by location of treatment (policy quirks)
    • Better imaging with little benefit
    • Proton treatment (for some conditions)
    • Heart stents
    • Arthroscopic knee surgery

Many estimates of “waste” are after-the-fact. It’s actually very hard to identify waste before-hand. Report on End-of-life Spending

Physician Agency

Definition

  • Physicians are better informed about treatment decisions than patients, and so there exists some agency relationship between the two. For many conditions, patients can’t treat themselves even if they wanted to.
  • Physicians also face incentives other than patient welfare, such as income, reputation, organizational pressures, and career advancement

Basic setup from McGuire (2000)

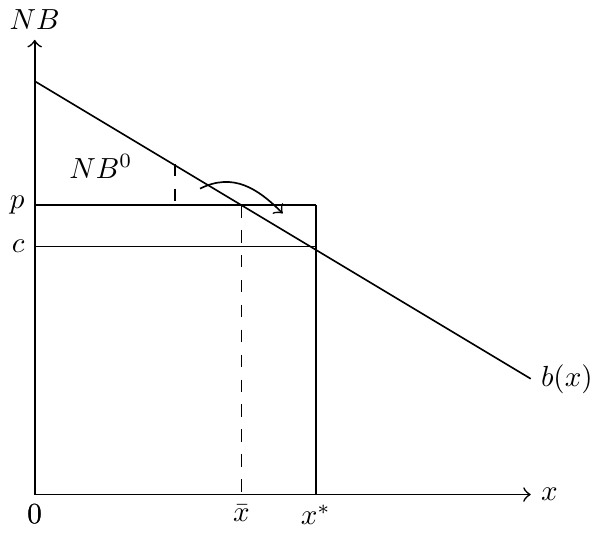
  • Denote quantity of physician services by \(x\)
  • Denote benefit of services to patient by \(B(x)\)
  • Patients pay (and physicians receive) a price of \(p\) for each unit of service \(x\)
  • Physicians incur cost \(c\) for each unit of care
  • Net benefit to patients is \(NB(x)=B(x)-px\)
  • Physicians must choose quantity of care at least better than the patient’s outside option, \(NB(x)= B(x)-px \geq NB^{0}\).

Solving the model

With this framework, how much care will be provided? What is the optimal value of \(x\)?

Solving the model

  • Patient’s objective: \[\max_{x} NB(x) = \max_{x} B(x) - px\]
  • Physician’s objective: \[\max_{x} \pi(x) = \max_{x} p x - c x \text{ s.t. } NB(x) \geq NB^{0}\]
  • Lagrangian: \[\mathcal{L} = p x - c x + \lambda (B(x) - p x - NB^{0})\]
  • First order conditions:

\[\begin{align} \frac{\partial \mathcal{L}}{\partial p} & = x - \lambda x = 0 \\ \frac{\partial \mathcal{L}}{\partial x} & = p - c + \lambda B'(x) - \lambda p = 0 \\ \frac{\partial \mathcal{L}}{\partial \lambda} &= B(x) - p x - NB^{0} = 0 \end{align}\]

\[\begin{align} \frac{\partial \mathcal{L}}{\partial p} & = x - \lambda x = 0 \\ \frac{\partial \mathcal{L}}{\partial x} & = p - c + \lambda B'(x) - \lambda p = 0 \\ \frac{\partial \mathcal{L}}{\partial \lambda} & = B(x) - p x - NB^{0} = 0 \end{align}\]

  • From the first equation, we have \(\lambda = 1\) (seller gains all surplus…any relaxation of surplus goes to profit)
  • From the second equation, we have \(B'(x)=c\) (seller will produce until marginal cost equals marginal benefit)
  • Compare to patient’s optimal, \(B'(x)=p\)

Physician agency in a graph

Agency with capitated payments

  • Physician receives fixed (“capitated”) amount for each patient, \(R\), along with some price per unit of service, \(p_{s}\)
  • Physician therefore paid \(R + (p_{s} - c)x\) for each patient
  • Number of patients for each physician expressed as a positive function of the net benefit offered, \(n(NB)\), where \(NB=B(x) - p_{d}x\). Here, we assume that the insurer sets \(p_{d}\) and \(p_{s}\) separately (the demand and supply price, respectively).
  • Physician again aims to maximize profits, \(\pi=n(NB)\left[R+(p_{s}-c)x\right]\).

Solution with capitated payments

Maximizing the profit function yields: \[n'(NB)(B'(x) - p_{d}) \left[R + (p_{s} - c)x \right] + n(NB)(p_{s}-c) = 0\]

Rearranging terms and multiplying both sides by \(\frac{1}{NB}\), we get: \[\frac{B'(x) - p_{d}}{NB} \frac{R + (p_{s} - c)x}{p_{s}-c} = - \frac{1}{\varepsilon_{n,NB}}\]

  1. What happens for \(R=0\)?
  2. What about \(R>0\), assuming \(p_{s}<c\)?

Problems with basic model

  • Setup from McGuire (2000) is useful as it introduces wedge between physician and patient optimums due solely to different costs faced by the two parties
  • But it’s not very flexible and it makes some strong assumptions about competition (outside options) and price setting/taking

Cutler et al. (2019)

Physicians aim to maximize: \[u_{ij} = \alpha B_{S}(x_{i}) + \beta \pi(x_{i}) - \delta_{d} (x_{i} - x_{i}^{D}) - \delta_{O}(x_{i} - x_{i}^{O}),\]

  • \(B_{S}(x_{i})\) is the perceived benefit to the patient, with utility weight \(\alpha\)
  • \(\pi(x_{i})\) is the physician’s profit and \(\beta\) the weight on profit in utility
  • \(x_{i}\) is the quantity of care provided
  • \(x^{D}\) and \(x^{O}\) are preferred quantities from an informed patient and from other organizational pressures, respectively
  • \(\delta_{d}\) and \(\delta_{O}\) are functions of the deviations from these preferred quantities

First order condition for \(x_{i}\) yields: \[\alpha B{'}_{S}(x_{i}) = - \beta \pi{'}(x_{i}) + \delta_{d}{'} + \delta_{O}{'}\]

\[\alpha B{'}_{S}(x_{i}) = - \beta \pi{'}(x_{i}) + \delta_{d}{'} + \delta_{O}{'}\]

  • Physician sets \(x_{i}\) to balance the marginal benefit to the patient with financial incentives, disutility from deviating from the patient’s preferred quantities, and disutility from organizational pressures
  • ‘Supplier-induced demand’
    • \(x>x^{D}\): Not really an issue as it could still be that \(B(x)>B(x^{D})\)
    • More narrowly, \(x>x^{D}\) and \(B(x)<B(x^{D})\)

Taking this to data

  • Impose functional form assumptions so that: \[u_{ij} = \alpha B(x_{i}) + \beta \pi x_{i} - \frac{\gamma_{D}}{2} (x_{i} - x_{i}^{D})^{2} - \frac{\gamma_{O}}{2} (x_{i} - x_{i}^{O})^{2}\]
  • Theoretical optimum: \[\alpha B{'}(x_{i}) = \beta \pi - \gamma_{D}(x_{i} - x_{i}^{D}) - \gamma_{O}(x_{i} - x_{i}^{O})\]
  • First-order taylor expansion of \(B{'}(x_{i})\) around \(\bar{x}\) yields: \[x_{i} = \bar{x} + Z_{i}^{D} + Z_{i}^{S} + \varepsilon_{i},\] so that observed treatment levels are a function of some mean value/starting point and demand and supply-side shifts

References

Cutler, David, Jonathan S. Skinner, Ariel Dora Stern, and David Wennberg. 2019. “Physician Beliefs and Patient Preferences: A New Look at Regional Variation in Health Care Spending.” American Economic Journal: Economic Policy 11 (1): 192–221. https://doi.org/10.1257/pol.20150421.
McGuire, Thomas G. 2000. “Physician Agency.” Handbook of Health Economics 1: 461–536.